gempy.core.solution.Solution

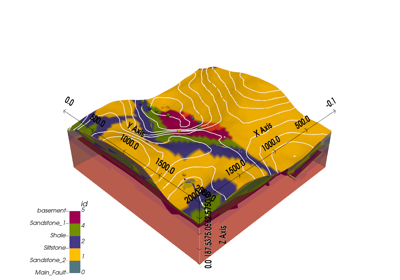
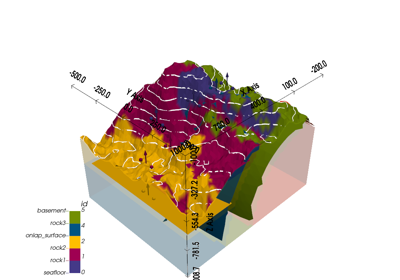
class gempy.core.solution.Solution(grid: Optional[gempy.core.data.Grid] = None, surfaces: Optional[gempy.core.data.Surfaces] = None, series: Optional[gempy.core.data_modules.stack.Series] = None)[source]

This class stores the output of the interpolation and the necessary objects to visualize and manipulate this data.

Depending on the activated grid (see Grid) a different number of

properties are returned returned:

Parameters

  • grid (Grid) – [s0] Class to generate grids.

  • surfaces (Surfaces) – [s1] Class that contains the surfaces of the model and the values of each of them.

  • series (Series) – [s2] Class that contains the functionality and attributes related to the series. Notice that series does not onlyrefers to stratigraphic series but to any set of surfaces which will be interpolated together (comfortably).

grid
Type

Grid

surfaces
Type

Surfaces

series
Type

Series

weights_vector

[s3] Numpy array that containing the kriging weights for each input data sorted by series

Type

numpy.array

scalar_field_at_surface_points

[s4] Value of the scalar field at each interface. Axis 0 is each series and axis 1 contain each surface in orde

Type

numpy.array

block_at_surface_points

[s5] 3D array with all interpolated values for a given series and at the interface

Type

numpy.array

mask_at_surface_points

[s6] Boolean array containing the logic to combine multiple series to obtain the final model at each interface

Type

numpy.array

values_at_surface_points

[s7] 2D array with the final values once the superposition of series has been carried out at each interface

Type

numpy.array

lith_block

[s8] Array with the id of each layer evaluated in each point of the regular grid.

Type

numpy.array

scalar_field_matrix

[s9] Value of the scalar field at each value of the regular grid.

Type

numpy.array

block_matrix

[s10] 3D array with all interpolated values for a given series and at each value of the regular grid.

Type

numpy.array

mask_matrix

[s11] Boolean array containing the logic to combine multiple series to obtain the final model at each value of the regular grid.

Type

numpy.array

mask_matrix_pad

mask matrix padded 2 block in order to guarantee that the layers intersect each other after marching cubes

Type

numpy.array

values_matrix

[s12] 2D array with the final values once the superposition of series has been carried out at each value of the regular grid

Type

numpy.array

vertices

[s13] List of numpy arrays containing the XYZ coordinates of each triangle vertex

Type

list[numpy.array]

edges

[s14] List of numpy arrays containing the indices of the vertices numpy arrays that compose each individual triangle.

Type

list[numpy.array]

geological_map

[s15] 2D array containing the lithologies at the surfaces.

Type

numpy.array

Examples using Solution

Methods

__init__([grid, surfaces, series])

Initialize self.

add_cartesian_coords(coords_base)

compute_all_surfaces(**kwargs)

Compute all surfaces of the model given the geological features rules.

compute_marching_cubes_regular_grid(level, …)

Compute the surface (vertices and edges) of a given surface by computing

create_struc_xarrays(values, l0, l1, res)

create_unstruct_xarray(values, l0, l1, xyz)

extract_each_surface_representations(ids, …)

padding_mask_matrix([mask_topography, shift])

Pad as many elements as in shift to the masking arrays. This is done

prepare_common_args(active_features, …)

prepare_marching_cubes_args(e, …)

set_meshes([surfaces])

Create xarray from the Surfaces object.

set_solution_to_custom(values)

set_solution_to_regular_grid(values[, …])

If regular grid is active set all the solution objects dependent on them and compute mesh.

set_solution_to_sections(values)

set_solution_to_topography(values)

set_solutions(sol, compute_mesh, sort_surfaces)

set_values(values[, active_features, …])

At this stage we should split values into the different grids

set_values_to_centered()

set_values_to_custom_grid(values, l0, l1, …)

set_values_to_regular_grid(values)

Set all solution values to the correspondent attribute.

set_values_to_regular_grid_(values, l0, l1, …)

set_values_to_sections(values, l0, l1, …)

set_values_to_surface_points(values)

set_values_to_surface_points_(values, l0, …)

set_values_to_topography(values, l0, l1, …)

set_vertices_edges(active_indices, s, s_n, v)

to_netcdf(path, name, **kwargs)

try_compute_marching_cubes_on_the_regular_grid(…)

Attributes

data_structures

__init__(grid: Optional[gempy.core.data.Grid] = None, surfaces: Optional[gempy.core.data.Surfaces] = None, series: Optional[gempy.core.data_modules.stack.Series] = None)[source]

Initialize self. See help(type(self)) for accurate signature.

set_solution_to_regular_grid(values: Union[list, numpy.ndarray], compute_mesh: bool = True, compute_mesh_options: Optional[dict] = None)[source]

If regular grid is active set all the solution objects dependent on them and compute mesh.

Parameters

  • values (list[np.array]) –

    list with result of the theano evaluation (values returned by gempy.compute_model() function):

    • block_matrix

    • weights_vector

    • scalar_field_matrix

    • scalar field at interfaces

    • mask_matrix

  • compute_mesh (bool) – if True perform marching cubes algorithm to recover the surface mesh from the implicit model.

  • compute_mesh_options (dict) – options for the marching cube function. - rescale: True

Returns

gempy.core.solutions.Solutions

set_values_to_regular_grid(values: Union[list, numpy.ndarray])[source]

Set all solution values to the correspondent attribute.

Parameters

  • values (np.ndarray) – values returned by function: gempy.compute_model function

  • compute_mesh (bool) – if true compute automatically the grid

Returns

gempy.core.solutions.Solutions

compute_marching_cubes_regular_grid(level: float, scalar_field, mask_array=None, rescale=False, **kwargs)[source]
Compute the surface (vertices and edges) of a given surface by computing

marching cubes (by skimage)

Parameters

  • level (float) – value of the scalar field at the surface

  • scalar_field (np.array) – scalar_field vector objects

  • mask_array (np.array) – mask vector with trues where marching cubes has to be performed

  • rescale (bool) – if True surfaces will be located between 0 and 1

  • **kwargs – skimage.measure.marching_cubes_lewiner args (see below)

Returns

vertices, simplices, normals, values

Return type

list

See also

skimage.measure.marching_cubes()

padding_mask_matrix(mask_topography=True, shift=2)[source]
Pad as many elements as in shift to the masking arrays. This is done

to guarantee intersection of layers if masked marching cubes are done

Parameters

  • mask_topography (bool) – if True mask also the topography. Default True

  • shift – Number of voxels shifted for the topology. Default 1.

Returns

masked regular grid

Return type

numpy.ndarray

compute_all_surfaces(**kwargs)[source]

Compute all surfaces of the model given the geological features rules.

Parameters

**kwargs – skimage.measure.marching_cubes args (see below)

Returns

vertices and edges

Return type

list

See also

gempy.core.solution.Solution.compute_marching_cubes_regular_grid()