1.3a: Grids.

import numpy as np
import matplotlib.pyplot as plt

import gempy as gp
from gempy.core.data import Grid
from gempy.core.data.grid_modules import RegularGrid

np.random.seed(55500)

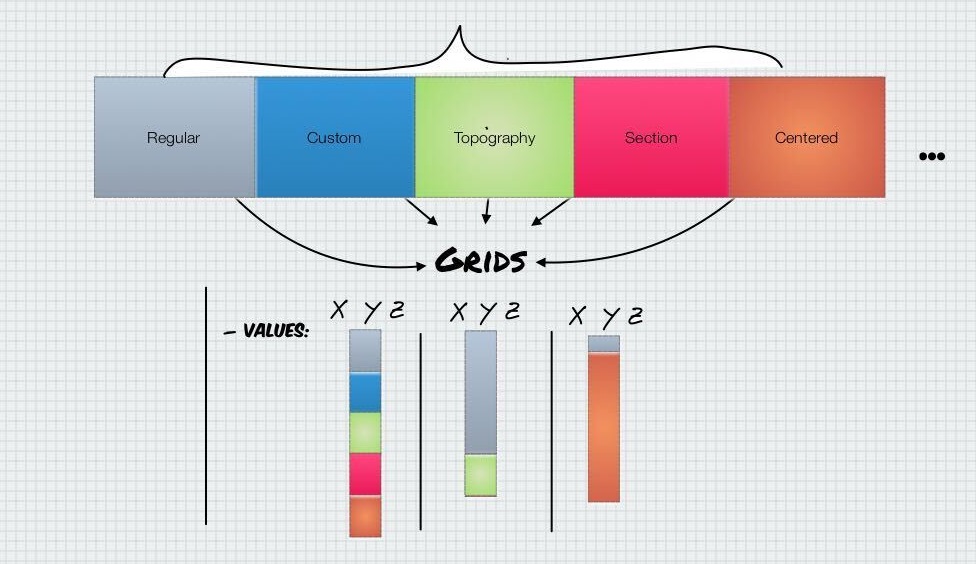
The Grid Class

The Grid class interacts with the rest of the data classes and grid subclasses. Its main purpose is to feed coordinates XYZ to the interpolator.

grid = Grid()

The most important attribute of Grid is values (and values_r which are the values rescaled) which are the 3D points in space that kriging will be evaluated on. This array will be fed by “grid types” on a composition relation with Grid:

print(grid.values)

[]

At the moment of writing this tutorial, there are 5 grid types. The number of grid types is scalable, and down the road we aim to connect other grid packages (like Discretize) as an extra Grid type.

This is an enum now

print(grid.GridTypes)

<enum 'GridTypes'>

Each grid contains its own values attribute as well as other methods to manipulate them depending on the type of grid.

print(grid.values)

[]

We can see which grids are activated (i.e. they are going to be interpolated and therefore will live on Grid().values) by:

print(grid.active_grids)

GridTypes.NONE

By default, only the regular grid (grid.regular_grid) is active. However, since the regular grid is still empty, Grid().values is empty too.

print(grid.values)

[]

The last important attribute of Grid is the length:

print(grid.length)

[]

Length gives back the interface indices between grids on the Grid().values attribute. This can be used after interpolation to know which interpolated values and coordinates correspond to each grid type. You can use the method get_grid_args to return the indices by name:

print(grid.topography)

None

By now all is a bit confusing because we have no values. Let’s start adding values to the different grids:

Regular Grid

The Grid class has a bunch of methods to set each grid type and activate them.

help(RegularGrid)

Help on class RegularGrid in module gempy.core.data.grid_modules.grid_types:

class RegularGrid(builtins.object)
 |  RegularGrid(extent: numpy.ndarray, resolution: numpy.ndarray, transform: Optional[gempy_engine.core.data.transforms.Transform] = None)
 |
 |  Class with the methods and properties to manage 3D regular grids where the model will be interpolated.
 |
 |  Methods defined here:
 |
 |  __eq__(self, other)
 |      Return self==value.
 |
 |  __init__(self, extent: numpy.ndarray, resolution: numpy.ndarray, transform: Optional[gempy_engine.core.data.transforms.Transform] = None)
 |      Initialize self.  See help(type(self)) for accurate signature.
 |
 |  __repr__(self)
 |      Return repr(self).
 |
 |  get_values_vtk_format(self, orthogonal: bool = False) -> numpy.ndarray
 |
 |  set_regular_grid(self, extent: Sequence[float], resolution: Sequence[int], transform: Optional[gempy_engine.core.data.transforms.Transform] = None)
 |      Set a regular grid into the values parameters for further computations
 |      Args:
 |          extent (list, np.ndarry):  [x_min, x_max, y_min, y_max, z_min, z_max]
 |          resolution (list, np.ndarray): [nx, ny, nz]
 |
 |  ----------------------------------------------------------------------
 |  Class methods defined here:
 |
 |  from_corners_box(pivot: tuple, point_x_axis: tuple, distance_point3: float, zmin: float, zmax: float, resolution: numpy.ndarray, plot: bool = True) from builtins.type
 |      Always rotate around the z axis towards the positive x axis.
 |      The distance_point3 is the distance from the pivot to the point3.
 |
 |  ----------------------------------------------------------------------
 |  Static methods defined here:
 |
 |  plot_rotation(regular_grid, pivot, point_x_axis, point_y_axis)
 |
 |  ----------------------------------------------------------------------
 |  Readonly properties defined here:
 |
 |  bounding_box
 |
 |  dx
 |
 |  dx_dy_dz
 |
 |  dy
 |
 |  dz
 |
 |  values_vtk_format
 |
 |  x_coord
 |
 |  y_coord
 |
 |  z_coord
 |
 |  ----------------------------------------------------------------------
 |  Data descriptors defined here:
 |
 |  __dict__
 |      dictionary for instance variables (if defined)
 |
 |  __weakref__
 |      list of weak references to the object (if defined)
 |
 |  transform
 |
 |  ----------------------------------------------------------------------
 |  Data and other attributes defined here:
 |
 |  __annotations__ = {'_transform': <class 'gempy_engine.core.data.transf...
 |
 |  __dataclass_fields__ = {'_transform': Field(name='_transform',type=<cl...
 |
 |  __dataclass_params__ = _DataclassParams(init=True,repr=True,eq=True,or...
 |
 |  __hash__ = None
 |
 |  __match_args__ = ('resolution', 'extent', 'values', 'mask_topo', '_tra...

extent = np.array([0, 100, 0, 100, -100, 0])
resolution = np.array([20, 20, 20])
grid.dense_grid = RegularGrid(extent, resolution)
print(grid.regular_grid)  # RegularGrid will return either dense grid or octree grid depending on what is set

RegularGrid(resolution=array([20, 20, 20]), extent=array([   0.,  100.,    0.,  100., -100.,    0.]), values=array([[  2.5,   2.5, -97.5],
       [  2.5,   2.5, -92.5],
       [  2.5,   2.5, -87.5],
       ...,
       [ 97.5,  97.5, -12.5],
       [ 97.5,  97.5,  -7.5],
       [ 97.5,  97.5,  -2.5]]), mask_topo=array([], shape=(0, 3), dtype=bool), _transform=None)

Now the regular grid object composed in Grid has been filled:

print(grid.regular_grid.values)

[[  2.5   2.5 -97.5]
 [  2.5   2.5 -92.5]
 [  2.5   2.5 -87.5]
 ...
 [ 97.5  97.5 -12.5]
 [ 97.5  97.5  -7.5]
 [ 97.5  97.5  -2.5]]

And the regular grid has been set active (it was already active in any case):

print(grid.active_grids)

GridTypes.NONE|DENSE

Therefore, the grid values will be equal to the regular grid:

print(grid.values)

[[  2.5   2.5 -97.5]
 [  2.5   2.5 -92.5]
 [  2.5   2.5 -87.5]
 ...
 [ 97.5  97.5 -12.5]
 [ 97.5  97.5  -7.5]
 [ 97.5  97.5  -2.5]]

And the indices to extract the different arrays:

print(grid.length)

[]

Custom Grid

Completely free XYZ values.

gp.set_custom_grid(grid, np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]))

Active grids: GridTypes.NONE|CUSTOM|DENSE

<gempy.core.data.grid_modules.grid_types.CustomGrid object at 0x7fda98ba4760>

Again, set_any_grid will create a grid and activate it. So now the composed object will contain values:

print(grid.custom_grid.values)

[[1 2 3]
 [4 5 6]
 [7 8 9]]

And since it is active, it will be added to the grid.values stack:

print(grid.active_grids)

GridTypes.NONE|CUSTOM|DENSE

print(grid.values.shape)

(8003, 3)

We can still recover those values with get_grid or by getting the slicing args:

print(grid.custom_grid)

<gempy.core.data.grid_modules.grid_types.CustomGrid object at 0x7fda98ba4760>

print(grid.custom_grid.values)

[[1 2 3]
 [4 5 6]
 [7 8 9]]

Topography

Now we can set the topography. Topography contains methods to create manual topographies as well as using gdal for dealing with raster data. By default, we will create a random topography:

gp.set_topography_from_random(grid)

[-20.   0.]
Active grids: GridTypes.NONE|TOPOGRAPHY|CUSTOM|DENSE

<gempy.core.data.grid_modules.topography.Topography object at 0x7fda98ba4310>

print(grid.active_grids)

GridTypes.NONE|TOPOGRAPHY|CUSTOM|DENSE

Now the grid values will contain both the regular grid and topography:

print(grid.values, grid.length)

[[  2.5          2.5        -97.5       ]
 [  2.5          2.5        -92.5       ]
 [  2.5          2.5        -87.5       ]
 ...
 [100.          89.47368421 -14.13839552]
 [100.          94.73684211 -16.12793911]
 [100.         100.         -16.21462612]] []

print(grid.topography.values)

[[  0.           0.         -14.23224119]
 [  0.           5.26315789 -14.18893341]
 [  0.          10.52631579 -13.54018217]
 ...
 [100.          89.47368421 -14.13839552]
 [100.          94.73684211 -16.12793911]
 [100.         100.         -16.21462612]]

We can compare it to the topography.values:

print(grid.topography.values)

[[  0.           0.         -14.23224119]
 [  0.           5.26315789 -14.18893341]
 [  0.          10.52631579 -13.54018217]
 ...
 [100.          89.47368421 -14.13839552]
 [100.          94.73684211 -16.12793911]
 [100.         100.         -16.21462612]]

Now that we have more than one grid, we can activate and deactivate any of them in real time:

grid.active_grids ^= grid.GridTypes.TOPOGRAPHY
grid.active_grids ^= grid.GridTypes.DENSE

Since now all grids are deactivated, the values will be empty:

print(grid.values)

[[1 2 3]
 [4 5 6]
 [7 8 9]]

grid.active_grids |= grid.GridTypes.TOPOGRAPHY

print(grid.values, grid.values.shape)

[[  1.           2.           3.        ]
 [  4.           5.           6.        ]
 [  7.           8.           9.        ]
 ...
 [100.          89.47368421 -14.13839552]
 [100.          94.73684211 -16.12793911]
 [100.         100.         -16.21462612]] (403, 3)

grid.active_grids |= grid.GridTypes.DENSE

print(grid.values)

[[  2.5          2.5        -97.5       ]
 [  2.5          2.5        -92.5       ]
 [  2.5          2.5        -87.5       ]
 ...
 [100.          89.47368421 -14.13839552]
 [100.          94.73684211 -16.12793911]
 [100.         100.         -16.21462612]]

Centered Grid

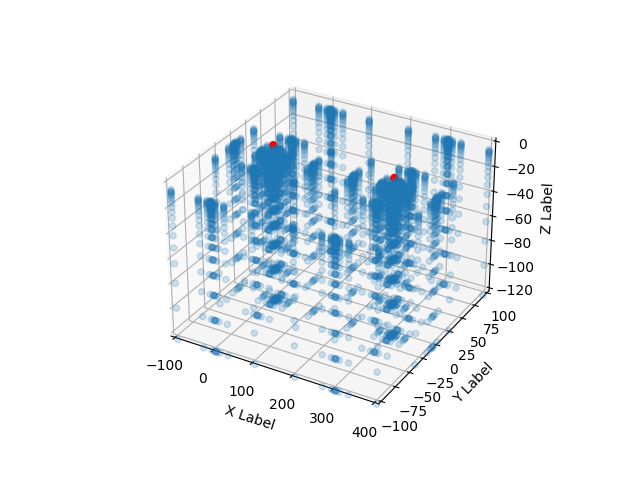
This grid contains an irregular grid where the majority of voxels are centered around a value (or values). This type of grid is usually used to compute certain types of forward physics where the influence decreases with distance (e.g. gravity: Check tutorial 2.2-Cell-selection )

gp.set_centered_grid(
    grid,
    centers=np.array([[300, 0, 0], [0, 0, 0]]),
    resolution=[10, 10, 20],
    radius=np.array([100, 100, 100])
)

Active grids: GridTypes.NONE|CENTERED|TOPOGRAPHY|CUSTOM|DENSE

CenteredGrid(centers=array([[300,   0,   0],
       [  0,   0,   0]]), resolution=[10, 10, 20], radius=array([100, 100, 100]), kernel_grid_centers=array([[-100.        , -100.        ,   -6.        ],
       [-100.        , -100.        ,   -7.2       ],
       [-100.        , -100.        ,   -7.52912998],
       ...,
       [ 100.        ,  100.        ,  -79.90178533],
       [ 100.        ,  100.        , -100.17119644],
       [ 100.        ,  100.        , -126.        ]]), left_voxel_edges=array([[ 34.1886117 ,  34.1886117 ,  -0.6       ],
       [ 34.1886117 ,  34.1886117 ,  -0.6       ],
       [ 34.1886117 ,  34.1886117 ,  -0.16456499],
       ...,
       [ 34.1886117 ,  34.1886117 ,  -7.95331123],
       [ 34.1886117 ,  34.1886117 , -10.13470556],
       [ 34.1886117 ,  34.1886117 , -12.91440178]]), right_voxel_edges=array([[ 34.1886117 ,  34.1886117 ,  -0.6       ],
       [ 34.1886117 ,  34.1886117 ,  -0.16456499],
       [ 34.1886117 ,  34.1886117 ,  -0.20970105],
       ...,
       [ 34.1886117 ,  34.1886117 , -10.13470556],
       [ 34.1886117 ,  34.1886117 , -12.91440178],
       [ 34.1886117 ,  34.1886117 , -12.91440178]]))

Resolution and radius create a geometrically spaced kernel (blue dots) which will be used to create a grid around each of the center points (red dots):

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.scatter(
    grid.centered_grid.values[:, 0],
    grid.centered_grid.values[:, 1],
    grid.centered_grid.values[:, 2],
    '.',
    alpha=.2
)

ax.scatter(
    np.array([[300, 0, 0], [0, 0, 0]])[:, 0],
    np.array([[300, 0, 0], [0, 0, 0]])[:, 1],
    np.array([[300, 0, 0], [0, 0, 0]])[:, 2],
    c='r',
    alpha=1,
    s=30
)

ax.set_xlim(-100, 400)
ax.set_ylim(-100, 100)
ax.set_zlim(-120, 0)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()

Section Grid

This grid type has its own tutorial. See 1.3b: 2-D sections